AB4 Endliche Automaten

Implementieren Sie die folgenden Funktionen nur unter Verwendung der bereits importierten Funktionen. Folgende Sprachkonstrukte dürfen nicht verwendet werden:

if ... then ... else ... (benutzen Sie stattdessen if' sofern importiert)
Guards
List Comprehensions: [(i,j) | i <- [1,2], j <- [3,4]]

Endliche Automaten

DFA (Deterministic Finite Automata)

Ein DFA besteht aus einem Alphabet $\Sigma$, einer Menge von Zuständen $Z$, einem Startzustand $z_0 \in Z$, einer Menge von Endzuständen $E \subseteq Z$ und einer totalen Überführungsfunktion $\delta \colon Z \times \Sigma \rightarrow Z$.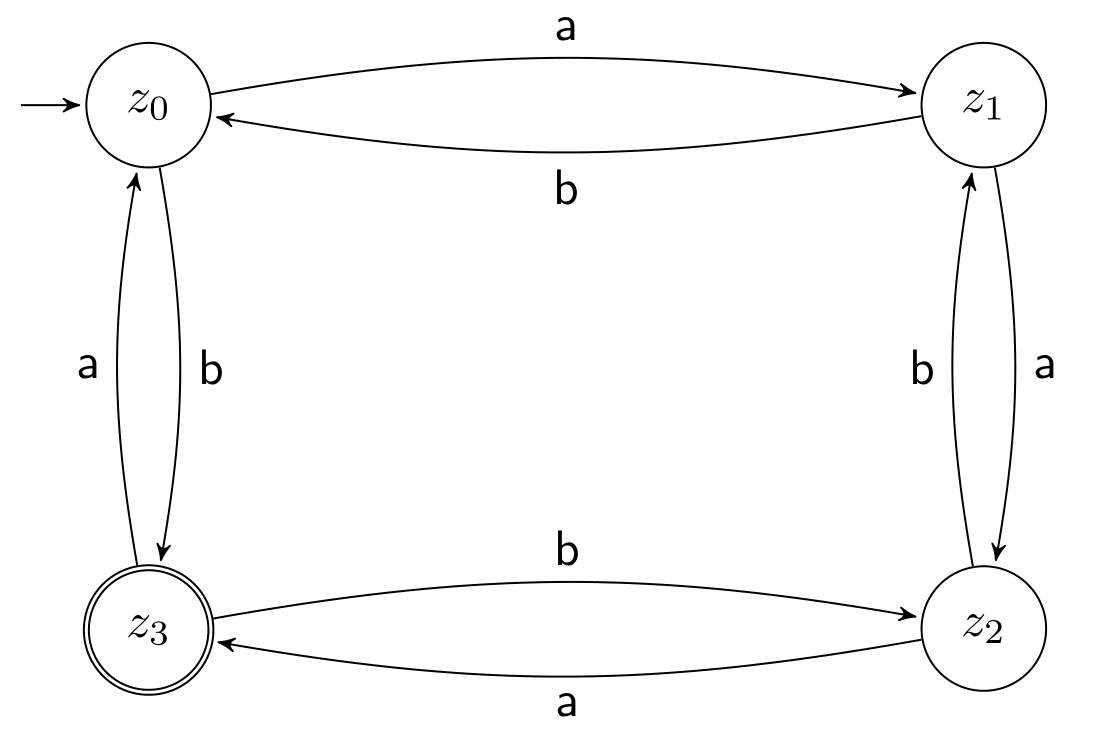

Quelle: Vorlesungsskript von H. Vollmer aus dem WiSe 19/20 zu Grundlagen der Theoretischen Informatik auf S. 8

Der obige Automat hat das Alphabet $\Sigma = \{a,b\}$, die Zustandsmenge $Z = \{z_0,z_1,z_2,z_3\}$, Startzustand $z_0$ und Endzustandsmenge $E = \{z_3\}$. Für die Eingabe $aaa$ durchläuft der Automat den Pfad von Zuständen $z_0, z_1, z_2, z_3$ und akzeptiert die Eingabe, weil der letzte Zustand im Pfad ein Endzustand ist. Für Eingabe $aaab$ durchläuft er die Zustände $z_0, z_1, z_2, z_3, z_2$ und akzeptiert diese Eingabe nicht. Die Sprache $L(M)$, die ein Automat $M$ erkennt, ist die Menge aller Wörter über $\Sigma$, welche von $M$ akzeptiert werden.

NFA (Non-Deterministic Finite Automata)

Ein NFA ist genauso definiert wie ein DFA, jedoch hat die Überführungsfunktion $\delta$ die Signatur $Z \times E \rightarrow \mathcal{P}(Z)$, wobei $\mathcal{P}(Z)$ die Menge aller Teilmengen von $Z$ bezeichnet. Das heißt, dass ein Zustand mehrere ausgehende Pfeile haben kann, welche das gleiche Symbol aus dem Alphabet enthalten. Es kann auch einen Zustand $z$ und ein Symbol $x$ geben, sodass es keinen ausgehenden Pfeil von $z$ gibt, welcher mit $x$ beschriftet ist (dies ist im DFA nicht möglich, da $\delta$ total sein muss).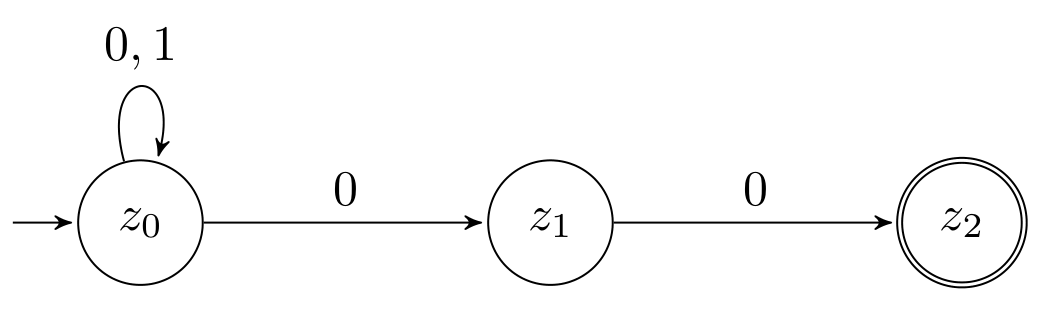

Quelle: Vorlesungsskript von H. Vollmer aus dem WiSe 19/20 zu Grundlagen der Theoretischen Informatik auf S. 10

Der obige NFA $M$ hat das Alphabet $\Sigma = \{0,1\}$. Beim Ausführen des NFA für eine Eingabe $x$ entsteht ein Baum $T_x$, welcher die nicht-deterministischen Wahlmöglichkeiten beschreibt. Für die Eingabe $0100$ und $001$ entstehen folgende Bäume:

Ein NFA akzeptiert eine Eingabe $x$ gdw. der Baum $T_x$ ein Blatt mit Tiefe $|x|$ enthält, welches ein Endzustand ist. Zum Beispiel akzeptiert der obige NFA die Eingabe $0100$, weil es ein Blatt $z_2$ mit Tiefe 4 gibt. Die Eingabe $001$ wird nicht akzeptiert, weil es kein Blatt $z_2$ mit Tiefe 3 gibt (nur mit Tiefe 2).

Codierung von DFA & NFA

type State       = String
type StartState  = State
type FinalStates = [State]
type DeltaFun    = Map (State,Char) State
type DeltaRel    = Map (State,Char) [State]

data DFA = DFA StartState FinalStates DeltaFun
data NFA = NFA StartState FinalStates DeltaRel

Es wird angenommen, dass $\Sigma$ gleich dem Datentyp Char ist. Somit ist jeder String eine gültige Eingabe. Die Menge der Zustände $Z$ ist implizit festgelegt als Bild von $\delta$ zusammen mit dem Startzustand $z_0$. Deshalb müssen $\Sigma$ und $Z$ bei der Definition eines Automaten in Code nicht angegeben werden. Falls die durch DeltaFun (bzw. DeltaRel) beschriebene Funktion nicht definiert ist für ein Tupel $(z,x)$, dann soll gelten $\delta(z,x) = z_{\text{undef}}$ (bzw. $\delta(z,x) = \emptyset$) , wobei $ z_{\text{undef}}$ ein spezieller Zustand ist, der durch die Konstante undefinedState repräsentiert wird, und $\emptyset$ die leere Menge.

Beispiele

m1 = DFA "z0" ["z3"]
  (fromList [
    (("z0",'a'),"z1"),
    (("z0",'b'),"z3"),
    (("z1",'a'),"z2"),
    (("z1",'b'),"z0"),
    (("z2",'a'),"z3"),
    (("z2",'b'),"z1"),
    (("z3",'a'),"z0"),
    (("z3",'b'),"z2")
  ] ) 
  
m2 = NFA "z0" ["z2"]  
  (fromList [
    (("z0",'0'),["z0","z1"]),
    (("z0",'1'),["z0"]),
    (("z1",'0'),["z2"])
  ])

Die Automaten m1 und m2 entsprechen dem DFA und NFA von oben.

nextState  :: DFA -> State -> Char -> State 
nextStates :: NFA -> State -> Char -> [State] 
isUndefinedTransition :: DFA -> State -> Char -> Bool

Die Funktion nextState gibt den nächsten Zustand vom DFA arg1 in Zustand arg2 beim Lesen vom Symbol arg3 zurück. Falls nichts definiert wurde, gibt sie undefinedState zurück. Zum Beispiel gibt (nextState m1 "z0" 'c') den Zustand undefinedState zurück.
Die Funktion nextStates gibt die nächsten möglichen Zustände vom NFA arg1 in Zustand arg2 beim Lesen vom Symbol arg3 zurück. Falls nichts definiert wurde, wird die leere Liste zurückgegeben. Zum Beispiel gibt (nextStates m2 "z1" '1') die leere Liste [] zurück.

-- a in {DFA, NFA}
startState   :: a -> State  
isFinalState :: a -> State -> Bool    
states       :: a -> [State]

Die Funktion startState gibt den Startzustand eines Automaten zurück.
Die Funktion isFinalState gibt zurück, ob arg2 ein Endzustand in arg1 ist.
Die Funktion states gibt die Menge aller Zustände von arg1 zurück.

Teil 1: Automaten ausführen

statePath :: DFA -> State -> String -> [State]
stateTree :: NFA -> State -> String -> Tree State

Die Funktion statePath gibt die Liste von Zuständen zurück, welche vom DFA arg1 im Zustand arg2 auf Eingabe arg3 durchlaufen wird. Falls arg3 leer ist, dann soll [arg2] zurückgegeben werden.
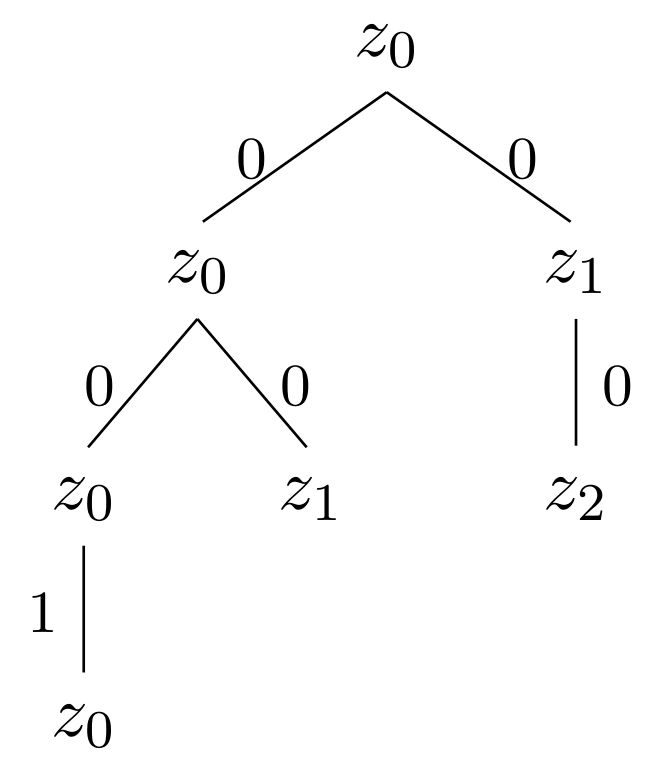
Die Funktion stateTree gibt den Baum von Zuständen zurück, welcher vom NFA arg1 in Zustand arg2 für die Eingabe arg3 erzeugt wird. Falls arg3 leer ist, dann soll Tree arg2 [] zurückgegeben werden.

inLanguageDFA :: DFA -> String -> Bool
inLanguageNFA :: NFA -> String -> Bool

Die Funktion inLanguageDFA gibt wahr zurück gdw. der DFA arg1 die Eingabe arg2 akzeptiert.
Die Funktion inLanguageNFA gibt wahr zurück gdw. der NFA arg1 die Eingabe arg2 akzeptiert.

isTotal :: DFA -> String -> Bool

Die Funktion isTotal gibt falsch zurück gdw. es eine Eingabe x gibt, die nur aus Zeichen aus arg2 besteht und für die gilt (last (statePath arg1 x)) == undefinedState. Sie können davon ausgehen, dass arg1 keine unerreichbaren Zustände besitzt.

Teil 2: Automaten kombinieren

single :: String -> DFA

Die Funktion single gibt einen Automaten zurück, welcher nur das Wort arg1 akzeptiert.

complement   :: String -> DFA -> DFA 
union        :: String -> DFA -> DFA -> DFA 
intersection :: String -> DFA -> DFA -> DFA

Die Funktion complement gibt einen Automaten zurück, welcher ein Wort x über dem Alphabet arg1 akzeptiert gdw. arg2 das Wort x nicht akzeptiert. Die kann realisiert werden, indem die Endzustände und nicht-Endzustände von arg2 vertauscht werden.
Die Funktion union gibt einen Automaten zurück, welcher ein Wort x über dem Alphabet arg1 akzeptiert gdw. arg2 oder arg3 das Wort x akzeptieren.
Die Funktion intersection gibt einen Automaten zurück, welcher ein Wort x über dem Alphabet arg1 akzeptiert gdw. arg2 und arg3 das Wort x akzeptieren.
Seien $M_1$ und $M_2$ DFA über dem Alphabet $\Sigma$. Der Produktautomat $M$ von $M_1$ und $M_2$ ist ein DFA, der wie folgt definiert ist. Die Zustandsmenge (bzw. Endzustandsmenge) von $M$ ist das Kreuzprodukt der Zustandsmengen (bzw. Endzustandsmengen) von $M_1$ und $M_2$. Der Startzustand von $M$ ist $(z_{01},z_{02})$, wobei $z_{01}$ und $z_{02}$ die Startzustände von $M_1$ und $M_2$ sind, respektive. Die Überführungsfunktion $\delta$ von $M$ ist wie folgt definiert für alle Zustände $z_1$ von $M_1$ und $z_2$ von $M_2$ und $x \in \Sigma$: $$ \delta((z_1,z_2),x) = (\delta_1(z_1,x),\delta_2(z_2,x)) $$ wobei $\delta_1$ und $\delta_2$ die Überführungsfunktion von $M_1$ und $M_2$ sind. Der Automat $M$ erkennt den Schnitt der Sprachen von $M_1$ und $M_2$.
Hinweis: der erste Parameter dieser drei Funktionen muss nur beachtet werden, wenn der Produktautomat berechnet wird.

Teil 3: Determinisierung

Die Potenzmengenkonstruktion ist ein Algorithmus, welcher einen NFA $M$ in einen DFA $M'$ umwandelt, sodass $ L(M) = L(M')$ (beide erkennen die gleiche Sprache). Dabei wird schrittweise eine Tabelle aus $M$ konstruiert, welche am Ende den DFA $M'$ beschreibt. Für den obigen NFA würde die Konstruktion dieser Tabelle wie folgt ablaufen:

Schritt 1/

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

beginne mit $\{z_0\}$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

von $z_0$ kommt man mit $0$ zu $z_0$ oder $z_1$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

von $z_0$ kommt man mit $1$ zu $z_0$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

füge $\{z_0,z_1\}$ hinzu, da es noch keine Zeile dafür gibt

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

betrachte für beide Zustände $z_0$ und $z_1$ die Übergänge

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

von $z_0$ kommt man mit 0 zu $z_0$ oder $z_1$, von $z_1$ kommt man mit 0 zu $z_2$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

von $z_0$ kommt man mit 1 zu $z_0$, von $z_1$ kommt man mit 1 zu keinem Zustand

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

füge $\{z_0,z_1,z_2\}$ hinzu, da es noch keine Zeile dafür gibt

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

betrachte für die Zustände $z_0, z_1, z_2$ die Übergänge

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

von $z_0$ kommt man mit 0 zu $z_0$ oder $z_1$ usw.

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

keine neuer Zustand taucht auf, also terminiert der Algorithmus

Die Zustände von $M'$ sind die Einträge in der ersten Spalte. Jeder Zustand von $M'$ entspricht einer Teilmenge der Zustände von $M$. Die Tabelle beschreibt die Überführungsfunktion von $M'$. Startzustand von $M'$ ist $\{z_0\}$. Die Menge der Endzustände von $M'$ besteht aus den Zuständen, die einen Endzustand von $M$ enthalten. In diesem Beispiel wäre nur $\{z_0, z_1, z_2\}$ ein Endzustand, weil $z_2$ ein Endzustand von $M$ ist.

determinize  :: String -> NFA -> DFA

Die Funktion determinize soll einen DFA zurückgegeben, welcher die gleiche Sprache erkennt wie arg2 über dem Alphabet arg1.

Teil 4: T9-Automat

T9 ist ein System, welches die Eingabe von Texten auf Endgeräten mit einer 12er-Tastatur (üblich auf alten Mobiltelefonen ohne Touchscreen) erleichtert. Den Ziffern 2 bis 9 werden disjunkte Teilmengen des Alphabets A-Z zugewiesen. Zusätzlich muss für die gewünschte Sprache ein Wörterbuch hinterlegt sein. Möchte der Nutzer nun z.B. "hallo" eingeben, so drückt er die Ziffern 4-2-5-5-6. Es kann vorkommen, dass unterschiedliche Wörter die gleiche Codesequenz haben. Zum Beispiel haben die Wörter "kiss" und "lips" beide die Codesequenz 5477. In diesem Fall kann man durch mehrmaliges Drücken einer bestimmten Taste das gewünschte Wort auswählen.

Für eine Liste von Wörtern (Wörterbuch) soll ein deterministischer Automat konstruiert werden, welcher für Strings über dem Alphabet 2-9 folgende Eigenschaften erfüllt.

der Automat akzeptiert eine Codesequenz gdw. diese mindestens ein Wort aus dem Wörterbuch beschreibt
sei z der letzte Zustand, welcher bei Ausführung des Automaten für eine Codesequenz x erreicht wird. Falls z ein Endzustand ist, dann soll gelten: (read z)::[String] ist die sortierte Liste der Wörter aus dem Wörterbuch, welche die Codesequenz x haben

t9dfa :: [String] -> DFA

Die Funktion t9dfa soll einen DFA, welcher die obigen Anforderungen erfüllt, für das Wörterbuch arg1 zurückgegeben. Sie können davon ausgehen, dass arg1 keine Duplikate enthält, nicht leer ist und auch nicht den leeren String enthält.

Tipp

Konstruieren Sie zuerst einen NFA, welcher für jedes Wort aus dem Wörterbuch einen Pfad hat.

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)