AB4 Finite Automata

Implement the following functions using only the already imported functions. Additionally, the following language constructs are not permitted:

if ... then ... else ... (use if' instead if imported)
Guards
List Comprehensions: [(i,j) | i <- [1,2], j <- [3,4]]

Finite Automata

DFA (Deterministic Finite Automata)

A DFA consists of an alphabet $\Sigma$, a set of states $Z$, a start state $z_0$, a set of final states $E \subseteq Z$ and a total transition function $\delta \colon Z \times \Sigma \rightarrow Z$.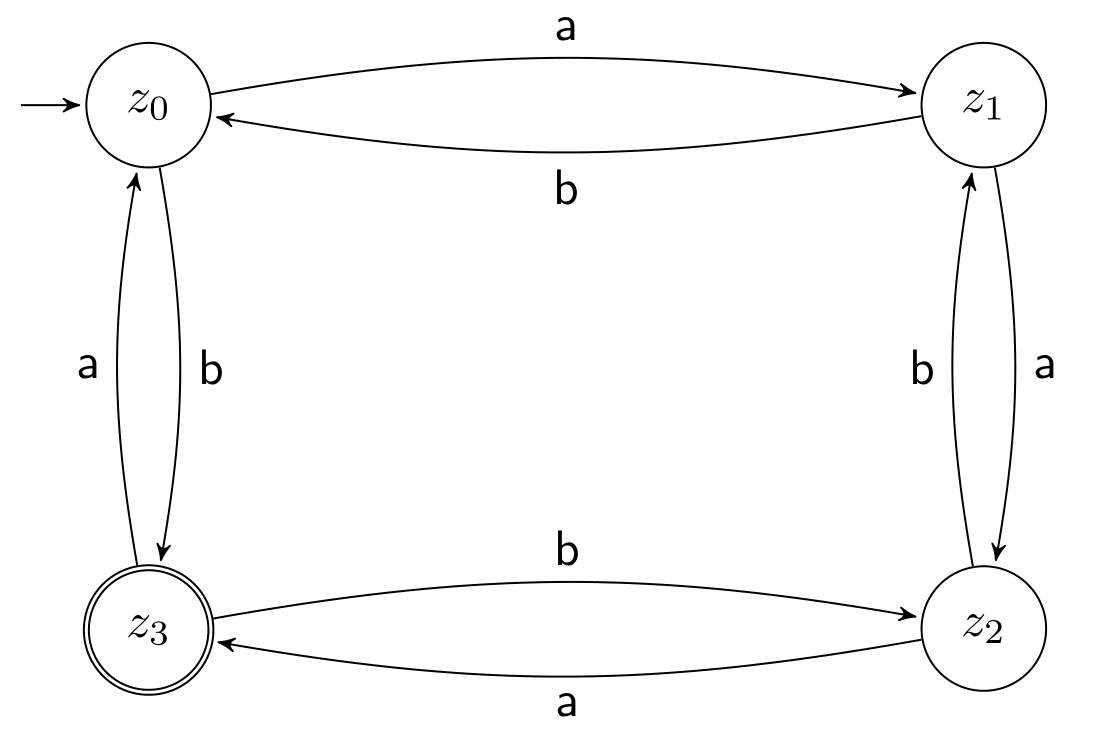

Source: Lecture notes Grundlagen der Theoretischen Informatik, H. Vollmer, WiSe 19/20, p. 8

The above automaton has alphabet $\Sigma = \{a,b\}$, the set of states $Z = \{z_0,z_1,z_2,z_3\}$, start state $z_0$ and the set of final states $E = \{z_3\}$. On input $aaa$ the automaton runs through the path of states $z_0, z_1, z_2, z_3$ and accepts the input because the last state in the path is a final state. On input $aaab$ the automaton runs through the states $z_0, z_1, z_2, z_3, z_2$ and rejects the input. The language $L(M)$ recognized by an automaton $M$ is the set of all words over $\Sigma$ which it accepts.

NFA (Non-Deterministic Finite Automata)

An NFA is defined just like a DFA with the exception that the transition function $\delta$ now has the signature $Z \times E \rightarrow \mathcal{P}(Z)$ where $\mathcal{P}(Z)$ denotes the set of all subsets of $Z$. This means that a state can have multiple outgoing edges which are labeled with the same symbol from the alphabet. It can also be the case that there is a state $z$ and a symbol $x$ such that there exists no outgoing edge from $z$ which is labeled with $x$ (this is not possible in a DFA because $\delta$ has to be total).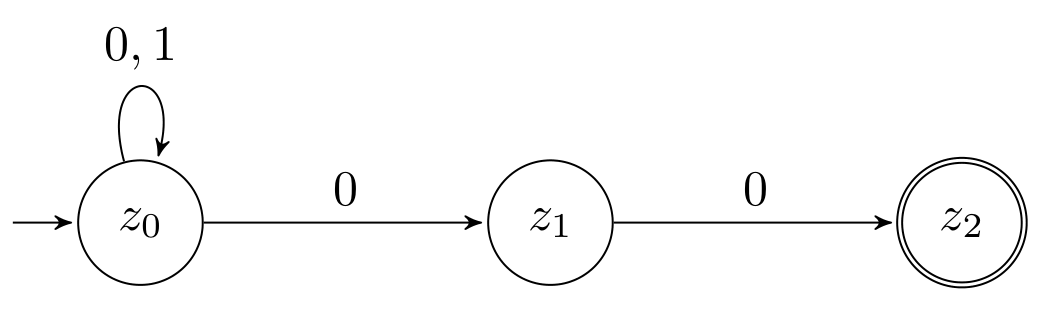

Source: Lecture notes Grundlagen der Theoretischen Informatik, H. Vollmer, WiSe 19/20, p. 10

The above NFA $M$ has alphabet $\Sigma = \{0,1\}$. The execution of an NFA on an input $x$ induces a tree $T_x$ which describes the non-deterministic moves that can be made by the automaton. Executing $M$ on the inputs $0100$ and $001$ induces the following trees, respectively:

An NFA accepts an input $x$ iff the tree $T_x$ has a leaf with depth $|x|$ which is a final state. For example, the above NFA accepts $0100$ because there is a leaf $z_2$ with depth 4. It does not accept $001$ because there is no leaf $z_2$ with depth 3 (only one with depth 2).

Encoding of DFA & NFA

type State       = String
type StartState  = State
type FinalStates = [State]
type DeltaFun    = Map (State,Char) State
type DeltaRel    = Map (State,Char) [State]

data DFA = DFA StartState FinalStates DeltaFun
data NFA = NFA StartState FinalStates DeltaRel

We assume that $\Sigma$ equals the data type Char. This means every String is a valid input. The set of states $Z$ is implicitly defined as the image of $\delta$ together with the start state $z_0$. Therefore $\Sigma$ and $Z$ can be omitted when defining an automaton in code. If the function described by DeltaFun (resp. DeltaRel) is not defined for a tuple $(z,x)$ then it shall hold that $\delta(z,x) = z_{\text{undef}}$ (resp. $\delta(z,x) = \emptyset$). The state $ z_{\text{undef}}$ is a special state which is represented by the constant undefinedState and $\emptyset$ denotes the empty set.

Beispiele

m1 = DFA "z0" ["z3"]
  (fromList [
    (("z0",'a'),"z1"),
    (("z0",'b'),"z3"),
    (("z1",'a'),"z2"),
    (("z1",'b'),"z0"),
    (("z2",'a'),"z3"),
    (("z2",'b'),"z1"),
    (("z3",'a'),"z0"),
    (("z3",'b'),"z2")
  ] ) 
  
m2 = NFA "z0" ["z2"]  
  (fromList [
    (("z0",'0'),["z0","z1"]),
    (("z0",'1'),["z0"]),
    (("z1",'0'),["z2"])
  ])

The automata m1 and m2 encode the above DFA and NFA.

nextState  :: DFA -> State -> Char -> State 
nextStates :: NFA -> State -> Char -> [State] 
isUndefinedTransition :: DFA -> State -> Char -> Bool

The function nextState returns the next state of the DFA arg1 in state arg2 when it reads the symbol arg3. If nothing is defined then it returns undefinedState. For example, (nextState m1 "z0" 'c') returns undefinedState.
The function nextStates returns the next possible states of the NFA arg1 in state arg2 when it reads the symbol arg3. If nothing is defined then it returns the empty list. For exampke, (nextStates m2 "z1" '1') returns [].

-- a in {DFA, NFA}
startState   :: a -> State  
isFinalState :: a -> State -> Bool    
states       :: a -> [State]

The function startState returns the start state of an automaton.
The function isFinalState returns true iff arg2 is a final state in arg1.
The function states returns the set of all states of arg1.

Part 1: Executing Automata

statePath :: DFA -> State -> String -> [State]
stateTree :: NFA -> State -> String -> Tree State

The function statePath returns the path of states which the DFA arg1 in state arg2 runs through on input arg3. If arg3 is empty then [arg2] should be returned.
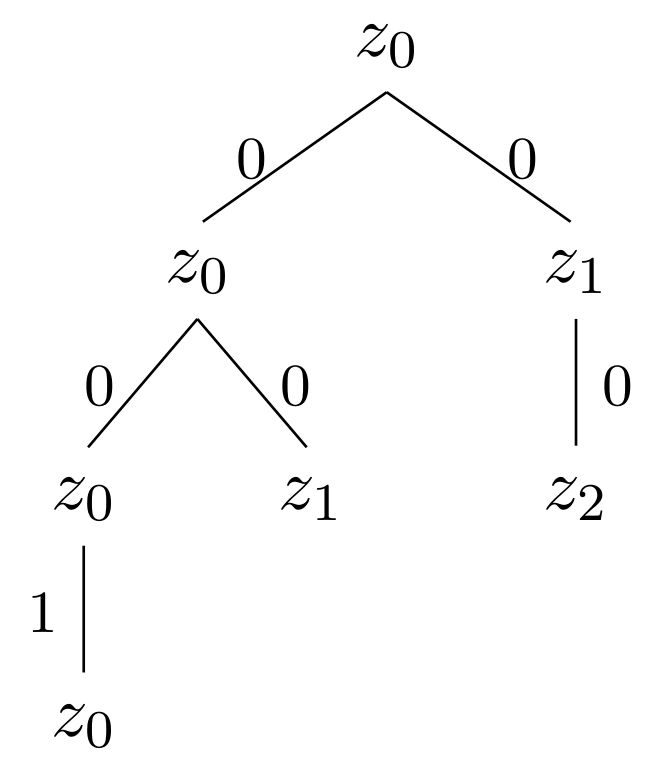
The function stateTree returns the tree which is induced by executing the NFA arg1 in state arg2 on input arg3. If arg3 is empty then Tree arg2 [] should be returned.

inLanguageDFA :: DFA -> String -> Bool
inLanguageNFA :: NFA -> String -> Bool

The function inLanguageDFA returns true iff the DFA arg1 accepts the input arg2.
The function inLanguageNFA returns true iff the NFA arg1 accepts the input arg2.

isTotal :: DFA -> String -> Bool

The function isTotal returns false iff there exists an input x which only consists of characters contained in arg2 and such that (last (statePath arg1 x)) == undefinedState. You may assume that arg1 does not contain unreachable states.

Part 2: Combining Automata

single :: String -> DFA

The function single returns a DFA which only accepts the input arg1.

complement   :: String -> DFA -> DFA 
union        :: String -> DFA -> DFA -> DFA 
intersection :: String -> DFA -> DFA -> DFA

The function complement returns a DFA which accepts an input x consisting only of characters contained in arg1 iff arg2 does not accept x. This can be realized by swapping the final states and non-final states of arg2.
The function union returns a DFA which accepts an input x consisting only of characters contained in arg1 iff arg2 or arg3 accepts x.
The function intersection returns a DFA which accepts an input x consisting only of characters contained in arg1 iff arg2 and arg3 accept x.
Let $M_1$ and $M_2$ be DFA over the alphabet $\Sigma$. The product automaton $M$ of $M_1$ and $M_2$ is a DFA, which is defined as follows. Its set of states (resp. set of final states) is the Cartesian product of the set of states (resp. the set of final states) of $M_1$ and $M_2$. Its start state is $(z_{01},z_{02})$ where $z_{01}$ and $z_{02}$ are the start states of $M_1$ and $M_2$, respectively. Its transition function $\delta$ is defined as follows for all states $z_1$ of $M_1$ and $z_2$ of $M_2$ and $x \in \Sigma$: $$ \delta((z_1,z_2),x) = (\delta_1(z_1,x),\delta_2(z_2,x)) $$ where $\delta_1$ and $\delta_2$ are the transition functions of $M_1$ and $M_2$. The automaton $M$ recognizes the intersection of the languages recognized by $M_1$ and $M_2$.
Hint: the first argument of these three functions is only relevant when defining the product automaton.

Part 3: Determinization

The powerset construction is an algorithm with which an NFA $M$ can be converted into a DFA $M'$ such that $ L(M) = L(M')$ (both recognize the same language). A table is constructed step by step from $M$ which eventually describes the DFA $M'$. For the above NFA the construction of this table looks as follows:

Step 1/

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

start with $\{z_0\}$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

given state $z_0$ and symbol $0$ the states $z_0$ and $z_1$ can be reached

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

given state $z_0$ and symbol $1$ the state $z_0$ can be reached

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

add $\{z_0,z_1\}$ because there is no row for it yet

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

consider the transitions for the two states $z_0$ and $z_1$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

given state $z_0$ and symbol 0 one can reach $z_0$ or $z_1$, given state $z_1$ and symbol 0 one can reach $z_2$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

given state $z_0$ and symbol 1 one can reach $z_0$, given state $z_1$ and symbol 1 no next state can be reached

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

add $\{z_0,z_1,z_2\}$ because there is no rows for it yet

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

consider the transitions for the states $z_0, z_1, z_2$

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

given state $z_0$ and symbol 0 one can reach $z_0$ or $z_1$ etc.

	$0$	$1$
$\{ z_0 \}$	$\{ z_0, z_1 \}$	$\{ z_0 \}$
$\{ z_0, z_1 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$
$\{ z_0, z_1, z_2 \}$	$\{ z_0, z_1, z_2 \}$	$\{ z_0 \}$

no new state occurs, therefore the algorithm terminates

The states of $M'$ are the entries in the first column. Each state of $M'$ is a subset of states of $M$. The table describes the transition function of $M'$. The start state of $M'$ is $\{z_0\}$. The set of final states of $M'$ consists of states which contain at least one final state from $M$. In this example the state $\{z_0, z_1, z_2\}$ is the only final state because $z_2$ is a final state in $M$.

determinize  :: String -> NFA -> DFA

The function determinize should return a DFA which recognizes the same language as arg2 over the alphabet arg1.

Part 4: T9-Automaton

T9 is a system intended to facilitate the input of texts on devices with a 3×4 numeric keypad (commonly found on old cellphones without touchscreen). The digits 2 through 9 are assigned non-overlapping subsets of the alphabet A-Z. Additionally, a dictionary for the desired language must be provided. For example, if the user wants to input "hello" then he presses the digits 4-2-5-5-6. It can occur that different words have the same code sequence. For example, the words "kiss" and "lips" both have the code sequence 5477. In such a case one can cycle through the possible options by repeatedly pressing a certain key.

Given a list of words (dictionary), a DFA should be constructed which satisfies the following properties for input strings which only consist of the digits 2 through 9.

the DFA accepts a code sequence iff it corresponds to at least one word from the dictionary
let z be the last state which the DFA reached on input x. If z is a final state then it should hold that (read z)::[String] is the sorted list of words from the dictionary which correspond to the code sequence x

t9dfa :: [String] -> DFA

The function t9dfa returns a DFA which satisfies the above conditions. You may assume that arg1 contains no duplicates, is not empty and does not contain the empty string.

Hint

First, construct an NFA which contains a path for each word from the dictionary.

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)

	\(0\)	\(1\)
\(\{ z_0 \}\)	\(\{ z_0, z_1 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)
\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0, z_1, z_2 \}\)	\(\{ z_0 \}\)