What is Shrimp?

Shrimp is a programming language to describe algorithms in terms of flow charts. In conventional programming languages the operations (lines of code which modify the contents of variables) and the control flow are intertwined. In contrast, Shrimp separates operations, the control flow and the predicates which guide it, thus encouraging to develop them separately. It is primarily aimed at programming novices in an educational context. However, it can also be used for implementing algorithms with complex control flows.

More precisely, Shrimp itself is not a full programming language but builds on top of the functional programming language Haskell. It is an embedded domain specific language which inherits the syntax of expressions and type system from its host language Haskell. A program written in Shrimp is called a Shrimp program or sp-program. The Shrimp compiler spc translates such a program into Haskell code and inserts it into a host Haskell source code file so that it becomes executable.

Shrimp programs can be translated such that when they are executed, a trace of the execution is written to the disk as a csv-file, which can be conveniently viewed with a spreadsheet application. Moreover, it provides functionality for comparing traces and also computing the code coverage.

Example

Given a string such as "abbbccaa" as input, return [('a',1),('b',3),('c',2),('a',2)], i.e. how often the same character appears consecutively. The following sp-program is an implementation of the straightforward algorithm which traverses the input string, counts the number of occurrences of the current character and when a new character appears (or the string ends), it appends this to the output.

#NAME
countAlg

#FUNCTIONS
count input = result

#VARIABLES
input  :: String --must be non-empty
result :: [(Char,Int)]
cur    :: Char
n      :: Int

#OPERATIONS
init:
  cur'    = first input
  n'      = 1
  input'  = removeFirst input
  result' = []

same: --same character as before
  n'     = n + 1
  input' = removeFirst input

new: --different character than before
  cur'    = first input
  n'      = 1
  input'  = removeFirst input
  result' = append (cur,n) result

final:
  result' = append (cur,n) result

#PREDICATES
hasNext = not (isEmpty input)
newChar = cur /= (first input)

#FLOW
init  = (hasNext (newChar new same) final)
same  = (hasNext (newChar new same) final)
new   = (hasNext (newChar new same) final)
final = HALT

Executing this program for "abbbccaa" produces the following trace (original csv-file):

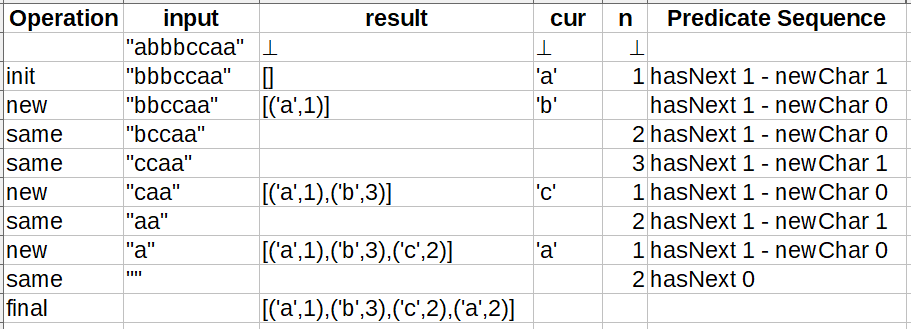
The first row after the headings describes the input values after calling the function count. The bottom symbol ⊥ indicates that a value has not been initialized (undefined). If a cell in a variable column is blank this means the value has not changed. Here is the coverage report for this single input.

Download

GHC

Shrimp requires the Glasgow Haskell Compiler (GHC). It can be downloaded from https://www.haskell.org/ghc. The quickest way to get started is to download the binaries of the current stable release and add the directory containing the binary file ghc to the $PATH variable. Alternatively, you can create symbolic links to ghc, ghci and runghc in a directory included in $PATH (e.g. /bin). Yet another alternative on Debian/Ubuntu is to use sudo apt-get install ghc which installs an older version of GHC (suffices to use Shrimp).

Alternatively, for a full installer and additional software commonly used with Haskell visit https://www.haskell.org and follow the instructions.

Shrimp

Download the current version 0.7.0.2:

• Shrimp 0.7.0.2 (zip-file)
• View documentation (also included in the zip)

Motivation

The following few paragraphs briefly explain the motivation and rationale behind Shrimp. In essence, its purpose is to aid in programming education and demonstrate that traces can be an effective means to implement and communicate algorithms.

An algorithm can have various representations. For example, it can be described informally in terms of algorithmic ideas or as code in some programming language. Another important form of representation is the mental representation of an algorithm that a person holds. Programming is the task of translating such a mental representation into a formal language. The converse direction, i.e. reading code and forming a mental representation of the underlying algorithm, is crucial if one wants to understand why it works correctly or how to modify it to achieve a certain goal.

The execution traces of an algorithm are another kind of representation, which can be used to construct a program and to facilitate understanding a program. Shrimp was designed such that code and traces are intimately connected. In fact, first there were traces and then the question what a program which generates such traces should look like. The reason for this is the insight that the mental representation of an algorithm (1) is closer to traces (2) than to code in some programming language (3). This means the conversion between (1) and (2) is easier than between (1) and (3). In fact, when going from (3) to (1) executing the code and thereby generating traces is common practice. The method linked above shows how to go from (1) to (3) via (2).

As a concrete example for going from (3) to (1) via (2), try to make sense of the previous sp-program (here) using only the trace that it produced. Even if you have never seen such unconventionally structured code before, understanding it shouldn't be difficult with a bit of programming experience due to the tight correspondence between sp-programs and their traces.

Giving programming novices more specific tasks can improve the learning experience and help identify deficits. For instance, with Shrimp it is possible to ask them to implement a certain algorithm that is specified in terms of its traces and an informal description. The traces could only contain the variable values (other columns are empty). In a simpler variant the operation column could be filled out as well. Their task would be to write an sp-program which generates matching traces. See the course material for Systematic Programming 2020 starting from AB3 Part 2 for some example tasks. An independent collection of tasks in this format is under development.

When searching for a basic algorithm such as BFS one can usually quickly find an animation of its execution. Such an animation helps to visualize the working principle of an algorithm. The information required to generate such an animation is present in the traces. To show the effectiveness of traces as means of communicating algorithms, an extension of Shrimp is planned which can generate animations of the execution from traces and also displays the relevant parts of the program alongside. Ideally, this can be used to present algorithms in a self-contained format.